Gamma rays are detected when atoms in a detector are ionized and the ions are collected either directly as in gaseous or semiconductor systems or by first conversion of the ionized electrons to light and subsequent conversion of the light to electrons in a photomultiplier tube (P-M tube or PMT). In all cases there is a voltage applied across some distance that causes a pulse to be created when a photon is absorbed.
The gamma rays are emitted according to Poisson statistics because each decaying nucleus is independent of the others and has an equal probability of decaying per unit time. Because the uncertainty in the production of gamma rays is therefore on the order of magnitude of the square root of the number of gamma rays, the more gamma rays that are detected, the less the proportional uncertainty will be. Thus sensitivity is a very important issue for the creation of images, since the rays will be detected by area. To get better resolution, one must have the numbers of counts and the apparatus to resolve them spatially. Having the large numbers of counts also means the apparatus must resolve them temporally.
The need for energy resolution carries its own burden. Depending on the detector, the energy resolution may be easily achieved or not (Table 13.3). In any case, the attenuation and scattering inside the body means that there will be a range of gamma rays emitted, and it will be difficult to tell those scattered through very small angles from those not scattered at all. This affects the spatial resolution of the instrument.
The current practice of nuclear medicine has defined the limits of the amount of activity that can be administered to a patient by the amount of radiation dose. Since planar imaging with one detector allows only 2 pi detection at best and generally a view of somewhat less because the source is in the patient and the lead collimation means that only rays that are directed from the decay toward the crystal will be detected, it is of utmost importance to detect every ray possible. To the extent that no one is ever satisfied with the resolution of any system and always wishes for better, there is the need to be able to get spatial resolution better than the intrinsic 2 mm currently achievable. Some better collimation system, such as envisioned in a coincidence detection system like that used in PET, might make it possible to avoid stopping so many of the rays with the collimator.
We have now seen that energy resolution, sensitivity and resolving time of the detector are all bound up together to produce the spatial resolution of the instrument as well as the more obvious temporal resolution. The need to collimate to create an image rather than a blush greatly decreases the numbers of counts and makes Poisson statistics a major determinant of the appearance of nuclear medical images.
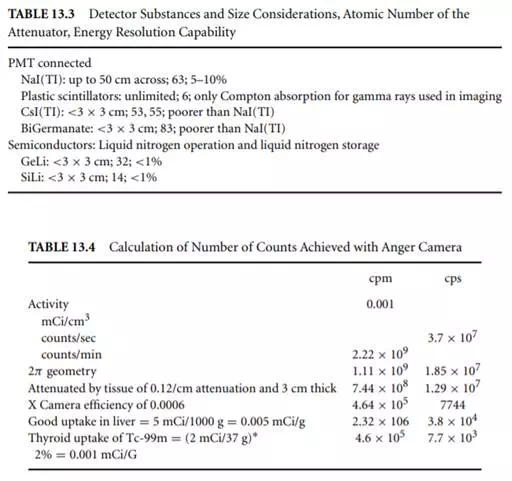
Table 13.4 shows a calculation for the NaI(TI)-based Anger camera showing 0.06% efficiency for the detection system. Thus the number of counts per second is not high and so is well within the temporal resolving capabilities of the detector system. The problem is the 0.06% efficiency, which is the effect of both the crystal thickness being optimized for imaging rather than for stopping all the gamma rays, and the lead collimation. Improvements in nuclear medicine imaging resolution can only come if both these factors are addressed.
