What is the finite element method
The finite element method (FEM) is a numerical technique for solving problems which are described by partial differential equations or can be formulated as functional minimization. A domain of interest is represented as an assembly of finite elements. Approximating functions in finite elements are determined in terms of nodal values of a physical field which is sought. A continuous physical problem is transformed into a discretized finite element problem with unknown nodal values. For a linear problem a system of linear algebraic equations should be solved. Values inside finite elements can be recovered using nodal values. Two features of the FEM are worth to be mentioned: 1) Piece-wise approximation of physical fields on finite elements provides good precision even with simple approximating functions (increasing the number of elements we can achieve any precision). 2) Locality of approximation leads to sparse equation systems for a discretized problem. This helps to solve problems with very large number of nodal unknowns.
How the FEM works
To summarize in general terms how the finite element method works we list main steps of the finite element solution procedure below.
Discretize the continuum. The first step is to divide a solution region into finite elements. The finite element mesh is typically generated by a preprocessor program. The description of mesh consists of several arrays main of which are nodal coordinates and element connectivities.
Select interpolation functions. Interpolation functions are used to interpolate the field variables over the element. Often, polynomials are selected as interpolation functions. The degree of the polynomial depends on the number of nodes assigned to the element.
Find the element properties. The matrix equation for the finite element should be established which relates the nodal values of the unknown function to other parameters. For this task different approaches can be used; the most convenient are: the variational approach and the Galerkin method.
Assemble the element equations. To find the global equation system for the whole solution region we must assemble all the element equations. In other words we must combine local element equations for all elements used for discretization. Element connectivities are used for the assembly process. Before solution, boundary conditions (which are not accounted in element equations) should be imposed.
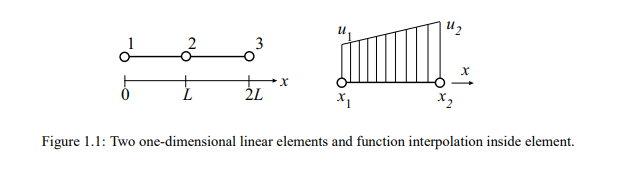
5. Solve the global equation system. The finite element global equation sytem is typically sparse, symmetric and positive definite. Direct and iterative methods can be used for solution. The nodal values of the sought function are produced as a result of the solution.
6. Compute additional results. In many cases we need to calculate additional parameters. For example, in mechanical problems strains and stresses are of interest in addition to displacements, which are obtained after solution of the global equation system.
Formulation of finite element equations
Several approaches can be used to transform the physical formulation of the problem to its finite element discrete analogue. If the physical formulation of the problem is known as a differential equation then the most popular method of its finite element formulation is the Galerkin method. If the physical problem can be formulated as minimization of a functional then variational formulation of the finite element equations is usually used.
Galerkin method Let us use simple one-dimensional example for the explanation of finite element formulation using the Galerkin method. Suppose that we need to solve numerically the following differential equation:
